学习机器学习

技术面问题

• GBDT的原理(理论基础）
• 决策树节点分裂时如何选择特征，写出Giniindex和InformationGain的公式并举例说明（理论基础）
• 分类树和回归树的区别是什么？（理论基础）
• ×GBoost的参数调优有哪些经验（工程能力）
• × GBoost 的 正 则 化 是 如 何 实 现 的 （ 工 程 能 力 ）

• × GBoost 的 并 行 化 部 分 是 如 何 实 现 的 （ 工 程 能 力 ）

• fast rcnn
• adaboost
• gbdt
• XGBOOST
  • xgboost，在求解速度，对异常值处理上要比gbdt要快
• random forest
• lgb
• 神经网络embedding层和w2v中的embedding的实现区别
• L1、L2的区别，L1为什么可以保证稀疏？
  • L1会让更多的参数变得稀疏，当参数很小时，这个参数的平方就可以被忽略，模型并不会进一步将这个参数调整为0
  • L1不可导，L2可导
• 深度学习的优化方法有哪些？ sgd、adam、adgrad区别？ adagrad详细说一下？为什么adagrad适合处理稀疏梯度？
• DL常用的激活函数有哪些？
• relu和sigmoid有什么区别，优点有哪些？
• 什么是梯度消失，标准的定义是什么？
• DNN的初始化方法有哪些？ 为什么要做初始化？ kaiming初始化方法的过程是怎样的？
• xgboost里面的lambdarank的损失函数是什么？
• xgboost在什么地方做的剪枝，怎么做的？
• xgboost如何分布式？特征分布式和数据分布式？ 各有什么存在的问题？
• lightgbm和xgboost有什么区别？他们的loss一样么？ 算法层面有什么区别？
• lightgbm有哪些实现，各有什么区别？
• EM
• LDA
• 要懂得算法的推导、适用场景、使用的Trick、分布式实现
• CNN、RNN、LSTM的基本原理，不同激活函数的差异等等，如果是面的传统机器学习岗的话，DL问的不深，但一定会问。
• softmax
• 逻辑斯蒂回归
• 逻辑斯蒂与softmax的关系
• 贝叶斯法则

• MLE 的假设（在机器学习判别模型中，假设所有的x都是均匀的，算极大似然的时候p(x,y)=P(x)p(y

  x)，所以可以直接算P(y

  x)。？（兰艳艳说的，对吗?））

• 机器学习面试题总结
• 交叉熵
• 梯度下降法的问题(不能全局最优，计算时间太长)
• SGD的问题(可能不能局部最优)
• 滑动平均模型
• KKT条件
• SVM 约束 求解 SMO 没看完
• 权重衰减 (代价函数中加入权重衰减项，代价函数变为严格凸函数)
• lr
• svm
• pr曲线
• 朴素贝叶斯 assumption / ensemble
• 决策树节点用哪个特征进行划分
• gbdt原理
• random forest 原理
• pca和lda降维原理
• k means 公式
• gmm 公式
• 特征选择的方法有哪些
• CNN 与 rnn的区别
• 距离度量的方式
• loss function
• 蓄水池抽样

深度学习

• bottleneck1 bottleneck2
• Mobilenetv2
• BP BP1
• 模型压缩
  • 压缩预训练模型。获得小型网络的一个办法是减小、分解或压缩预训练网络，例如量化压缩(product quantization)、哈希(hashing )、剪枝(pruning)、矢量编码( vector quantization)和霍夫曼编码(Huffman coding)等；此外还有各种分解因子(various factorizations )用来加速预训练网络；还有一种训练小型网络的方法叫蒸馏(distillation )，使用大型网络指导小型网络。
  • 直接训练小型模型。 例如Flattened networks利用完全的因式分解的卷积网络构建模型，显示出完全分解网络的潜力；Factorized Networks引入了类似的分解卷积以及拓扑连接的使用；Xception network显示了如何扩展深度可分离卷积到Inception V3 networks；Squeezenet 使用一个bottleneck用于构建小型网络。
  • MobileNet网络架构，允许模型开发人员专门选择与其资源限制(延迟、大小)匹配的小型模型，MobileNets主要注重于优化延迟同时考虑小型网络，从深度可分离卷积的角度重新构建模型
  • 深度可分离卷积干的活是：把标准卷积分解成深度卷积(depthwise convolution)和逐点卷积(pointwise convolution)。
  • MobileNetVI的创新点在于用深度可分离卷积（depthwiseseparableconvolution)代替传统的卷积操作，这样可以减少参数的数量和操作，但同时会使特征丢失导致精度下降。为了解决上述问题，MobileNet\/2在深度可分离卷积的基础上，使用倒残差(InvertedResidual)和线性瓶fi(LinearBottleneck）技术来保持模型的表征能力。
• Batch-normalization
• 多通道卷积 (分别相乘再求和)
• 视频语义分割

  • PSP-net使用了resnet101作为网络的backbone,提出了使用pyramidpoolingmodu

    e即特征网络金子塔结构作为conte×tmode

    ing来获取不同尺度的信息

  • Deeplabv3同样使用resnetl01作为网络的backbone,提出了ASPP的结构，通过不同dilationrate的卷积操作来获取不同尺度的context的信息以及结合全局的context(图中ImagePooling)的融合进一步地提高特征的表征能力。
• 目标检测的二阶段模型
  • R-CNN:R-CNN系列的开山之作
  • FastR-CNN:共享卷积运算
  • FasterR-CNN： 两阶段模型的深度化
  • SSD:Single Shot Multibox Detector
• Deeplabv3+
  • 论文提出的DeepLabv3+是encoder-decoder架构，其中encoder架构采用DeepLabv3，decoder采用一个简单却有效的模块用于恢复目标边界细节。并可使用扩张卷积在指定计算资源下控制feature的分辨率。
  • 论文探索了Xception和深度分离卷积在模型上的使用，进一步提高模型的速度和性能。模型在VOC2012上获得了新的state-of-the-art表现。
• 1*1卷积核有什么用 (增加/减少通道)
  • 卷积核的个数就对应输出的通道数（channels），这里需要说明的是对于输入的每个通道，输出每个通道上的卷积核是不一样的。比如输入是28x28x192(WxDxK,K代表通道数)，然后在3x3的卷积核，卷积通道数为128，那么卷积的参数有3x3x192x128，其中前两个对应的每个卷积里面的参数，后两个对应的卷积总的个数（一般理解为，卷积核的权值共享只在每个单独通道上有效，至于通道与通道间的对应的卷积核是独立不共享的，所以这里是192x128）。
• CNN 为什么能给物品分类？ (卷积层+完全连接层,表征图像然后将特征和标签联系起来)
  • 学习到的核权重倾向于将相似的对象映射到同一个区域。学习到的锚向量 A 将所有代表猫特征的向量 X_cat 映射为 Y_cat，而其它代表狗特征的向量 X_dog 或代表车特征的向量 X_car 将永远不会出现在这个区域。这就是 CNN 能够有效识别不同对象的原因。
  • 通常 CNN 被分解为两个子网络：特征提取(FE)子网络和决策(DM)子网络。FE 子网络由多个卷积层组成，而 DM 子网络由几个完全连接层组成。简而言之，FE 子网络通过一系列 RECOS 变换以形成用于聚类的新表征。DM 子网络将数据表征与决策标签联系起来，它的作用与 MLP 的分类作用类似。
  • CNN 可以自动提取特征并且基于这些特征学习分类输入数据，而随机森林(RF)和支持向量机(SVM)则非常依赖于特征工程，而这种特征工程往往很难操作。
• 图像上采样
  • 几乎都是采用内插值法，即在原有图像像素的基础上，在像素点值之间采用合适的插值算法插入新的元素；
  • 反卷积方法（Deconvolution），又称转置卷积法(Transposed Convolution)；反转置矩阵 416 的矩阵乘以 161 得到 4*1 得到下采样的矩阵
  • 反池化方法（Unpooling）。
• 交叉熵
  • 交叉熵损失是每一个样本（或者图像中每一个像素的交叉熵的和）
• Softmax+交叉熵
  • 神经网络最后一层得到每个类别的得分scores，该得分经过softma×转换为概率输出，模型预测的类别概率输出与真实类别的。onehot形式进行crossentropy损失函数的计算。
• 视频分析
  • 视频分析1
  • 视频行为识别 （传统方法 密集采样特征点/轨迹与轨迹描述子/运动描述子， TWO STREAM方法 TWO-STREAM CNN/TSN， C3D方法，RNN方法）
• 常见图模型

  • 有向图（静态贝叶斯网络

    动态贝叶斯网络（隐马尔可夫模型

    卡尔曼滤波器））

  • 无向图 （马尔可夫网络（吉布斯

    玻尔兹曼机

    条件随机场））

• dropout
• attention
  • Attention机制其实就是一系列注意力分配系数，也就是一系列权重参数罢了。

无监督学习

• 无监督学习的优势
  • Raw data cheap. Labeled data expensive.
  • Save memory/computation.
  • Reduce noise in high-dimensional data.
  • Useful in exploratory data analysis.
  • Often a pre-processing step for supervised learning.
• 技术
  • 自编码机(Autoencoding)
  • 随机森林(Random forests)
  • 主成分分析(PCA)
  • 随机森林(Random forests)
  • GAN
• 聚类的类型
  • 分层聚类 & 划分聚类
• GMM VS K-Means
  • K-means
    • Loss function: minimize sum of squared distance.
    • Hard assignment of points to clusters.
    • Assumes spherical clusters with equal probability of a cluster.
  • GMM
    • Minimize negative log likelihood.
    • Soft assignment of points to clusters.
    • Can be used for non-spherical clusters with different probabilities.
• 分层聚类中各种类间距离度量的优劣
  • MIN Advantage: Non-spherical, non-convex clusters Problem: Chaining
  • MAX Advantage: more robust against noise (no chaining) Problem: Tends to break large clusters,
• DBSCAN
  • Advantages （Not need to specify the number of clusters / Arbitrary shape cluster / Robust to outliers ）
  • Disadvantages （Difficult parameter selection (MinPts,E) /Not proper for data sets with large differences in densities ）
• 特征选择和特征提取
  • 什么是维度爆炸 （当数据的维度非常大的时候，点与点之间的距离和密度将会变得非常没有意义，最近距离几乎等于最远距离，意味着所有点之间的距离几乎相等。）
  • 什么是维度约减 （将高维数据映射到低维空间 基本想法：数据本质上的维度就是比较小的，或者与学习相关的维度是小的）

  • PCA的优点和缺点 （Eigenvector method / No tuning parameters / Non-iterative / No local optima

    Limited to second order statistics / Limited to linear projections）

  • NMF（非负矩阵分解）
  • 非线性的特征提取（）
    • Metric MDS and Isomap compute embeddings that seek to preserve interpoint straight-line (Euclidean) distances or geodesic distances between all pairs of points. Hence they are global methods.
    • Both locally linear embedding (LLE) and Laplacian eigenmap try to recover the global nonlinear structure from local geometric properties. They are local methods.
    • Overlapping local neighborhoods, collectively analyzed, can provide information about the global geometry.
  • 小结 （Dimension Reduction: mapping of the original high-dim data into a lower-dim space）
    • Main idea: Minimization of reconstruction error / Maximization of variance。
    • Algorithms: Linear (PCA, NME, RP) / Non-linear (KPCA, LLE, LE)
    • Beyond: Robust, probabilistic, sparse …
    • 主成分分析（Principal Component Analysis,PCA)、线性判别分析（Linear Discriminant Analysis,LDA）、等距映射（Isomap）、局部线性嵌入（Locally Linear Embedding,LLE）、Laplacian 特征映射（Laplacian Eigenmaps）、局部保留投影（Local Preserving Projection,LPP）、局部切空间排列（Local Tangent Space Alignment,LTSA）、最大方差展开（ Maximum Variance Unfolding,MVU）
    • 线性降维方法主要包括PCA、LDA、LPP（LPP其实是Laplacian Eigenmaps的线性表示）；非线性降维一类是基于核的，如KPCA，此处暂不讨论；另一类就是通常所说的流形学习：从高维采样数据中恢复出低维流形结构（假设数据是均匀采样于一个高维欧式空间中的低维流形），即找到高维空间中的低维流形，并求出相应的嵌入映射。非线性流形学习方法有：Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU整体来说，线性方法计算块，复杂度低，但对复杂的数据降维效果较差。
    • 监督式和非监督式学习的主要区别在于数据样本是否存在类别信息。非监督降维方法的目标是在降维时使得信息的损失最小，如PCA、LPP、Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU；监督式降维方法的目标是最大化类别间的辨别信，如LDA。事实上，对于非监督式降维算法，都有相应的监督式或半监督式方法的研究。
    • 全局方法不仅考虑样本几何的局部信息，和考虑样本集合的全局信息，及样本点与非临近点之间的关系。全局算法有PCA、LDA、Isomap、MVU。

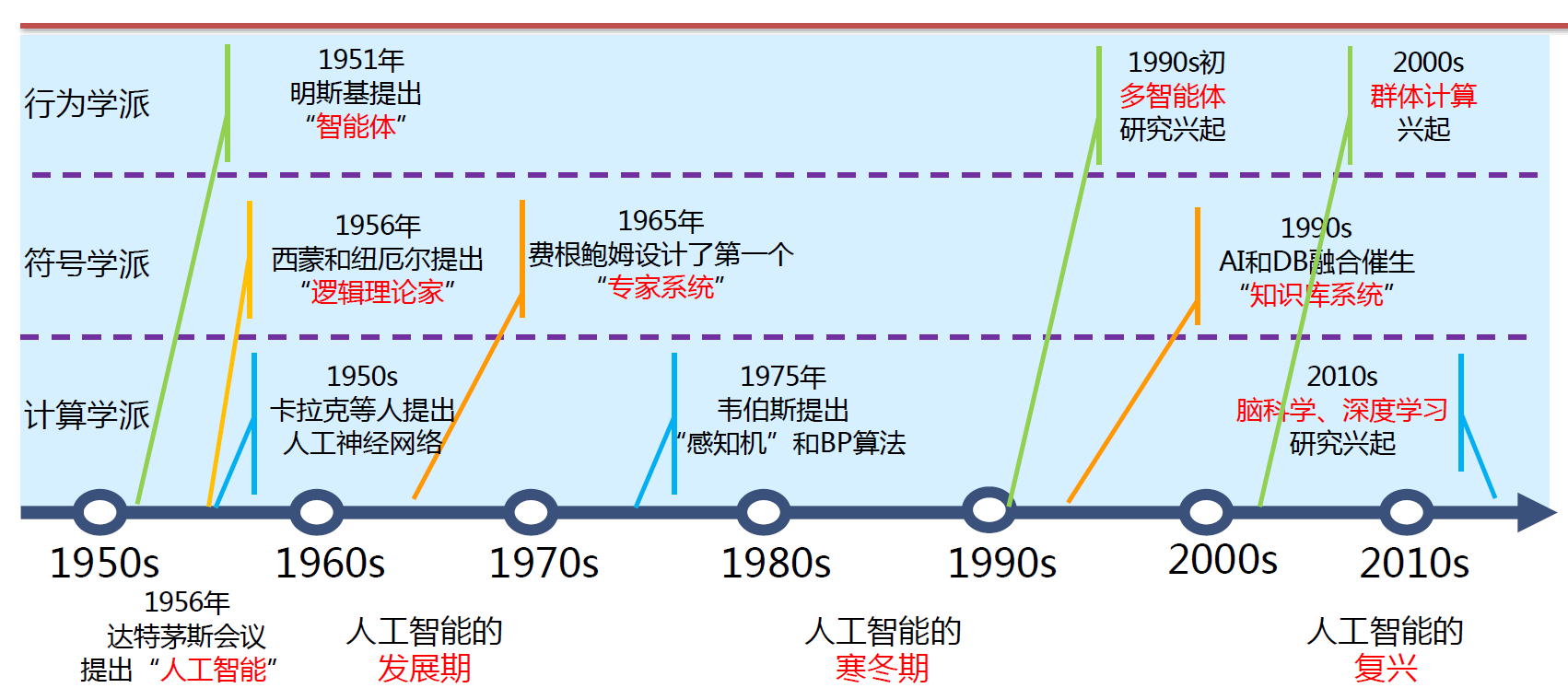
人工智能

• “智能”本身就没有明确的定义
• 计算机领域的人工智能指对“智能代理“的研究，可以是硬件、软件，可以感知环境、采取行动以能达到其特定目标的任何设备都是智能代理。
• 为什么下围棋进展如此快？
  • 因为下围棋可以由机器自己判定输赢，因此可以大量的模拟，增强学习。但像语音识别和人脸识别等是不能由机器自己判定的，需要人来判定，因此不能采用增强学习。增强学习不能在感知类问题上使用。
• 人工智能为什么火了起来？
  • A+B+C 算法 大数据 计算力
• Haar like 特征在特征提取中人工选用的是1 1 -1 -1 矩阵可以表示两个部分的图像相减，而在CNN中，这个1 1 -1 -1 是学习得到的。
• 人工智能以后？小样本学习方法？
• 相关
  • 奇点临近/人工智能时代/Our Final Invention 终极发明/超级智能/终极算法 The Master Algorithm
  • Her/人工智能/我，机器人/鹰眼/超能陆战队/机械姬
  • 新智元/机器之心/36氪

数据挖掘

• 数据挖掘十大算法
• KNN
• [什么是过拟合，泛化性？并分析两者的联系和区别]
  • 为了得到一致假设而使假设变得过度复杂称为过拟合。 想像某种学习算法产生了一个过拟合的分类器， 这个分类器能够百分之百的正确分类样本数据 （即再拿样本中的文档来给它，它绝对不会分错） ，但也就为了能够对样本完全正确的分类，使得它的构造如此精细复杂， 规则如此严格， 以至于任何与样本数据稍有不同的文档它全都认为不属于这个类别。
  • 一个假设能够正确分类训练集之外数据 （即新的， 未知的数据） 的能力称为该假设的泛化性。
• 请分析特征选择和特征提取有何区别？
  • 特征选择定义为从有 N 个特征的集合中选出具有 M 个特征的子集，并满足条件 M≤N。特征选择能够为特定的应用在不失去数据原有价值的基础上选择最小的属性子集，去除不相关的和冗余的属性。
  • 特征提取广义上指的是一种变换， 将处于高维空间的样本通过映射或变换的方式转换到低维空间， 达到降维的目的。 它可以从一组特征中去除冗余或不相关的特征来降维。
• 试分析回归和分类的区别？
  • 分类问题和回归问题都要根据训练样本找到一个实值函数 g(x)。回归问题的要求是：给定一个新的模式，根据训练集推断它所对应的输出 y（实数）是多少。也就是使用 y=g(x)来推断任一输入 x 所对应的输出值。分类问题是： 给定一个新的模式，根据训练集推断它所对应的类别（如： +1，-1）。也就是使用
  • y=sign(g(x))来推断任一输入 x 所对应的类别。 综上，回归问题和分类问题的本质一样，不同仅在于他们的输出的取值范围不同。 分类一般针对离散型数据而言的，回归是针对连续型数据的，但是其实本质上是一样的。
• 数据挖掘的完整流程是什么？
  • （1）数据理解：数据理解阶段从初始的数据收集开始，通过一些活动的处理，目的是熟悉数据，识别数据的质量问题，首次发现数据的内部属性，或是探测引起兴趣的子集去形成隐含信息的假设。
  • （2）数据准备： 数据准备阶段包括从未处理数据中构造最终数据集的所有活动。 这些数据将是模型工具的输入值。 这个阶段的任务有个能执行多次， 没有任何规定的顺序。 任务包括表、 记录和属性的选择，以及为模型工具转换和清洗数据。
  • （3）建模：在这个阶段，可以选择和应用不同的模型技术， 模型参数被调整到最佳的数值。 一般，有些技术可以解决一类相同的数据挖掘问题。 有些技术在数据形成上有特殊要求， 因此需要经常跳回到数据准备阶段。
  • （4）评估： 到项目的这个阶段，你已经从数据分析的角度建立了一个高质量显示的模型。 在开始最后部署模型之前， 重要的事情是彻底地评估模型， 检查构造模型的步骤， 确保模型可以完成业务目标。 这个阶段的关键目的是确定是否有重要业务问题没有被充分的考虑。 在这个阶段结束后， 一个数据挖掘结果使用的决定必须达成。
  • （5）部署：通常，模型的创建不是项目的结束。模型的作用是从数据中找到知识， 获得的知识需要便于用户使用的方式重新组织和展现。根据需求，这个阶段可以产生简单的报告，或是实现一个比较复杂的、 可重复的数据挖掘过程。
• 请描述 EM 算法原理和技术。
  • EM 算法是一种迭代算法 ,主要用来计算后验分布的众数或极大似然估计 ,广泛地应用于缺损数据、截尾数。在统计计算中，最大期望（ EM）算法是在概率（ probabilistic）模型中寻找参数最大似然估计或者最大后验估计的算法， 其中概率模型依赖于无法观测的隐藏变量（ Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（ Data Clustering）领域。最大期望算法经过两个步骤交替进行计算：第一步是计算期望（ E），利用对隐藏变量的现有估计值，计算其最大似然估计值； 第二步是最大化 （M），最大化在 E 步上求得的最大似然值来计算参数的值。 M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。总体来说， EM 的算法流程如下： 1.初始化分布参数 2.重复直到收敛： E 步骤：估计未知参数的期望值，给出当前的参数估计。 M 步骤：重新估计分布参数，以使得数据的似然性最大，给出未知变量的期望估计。据成群数据、带有讨厌参数的数据等所谓的不完全数据的统计推断问题。

NLP

• 机器阅读
  • 几乎所有做SQuAD的模型都可以概括为同一种框架：Embed层，Encode层，Interaction层和Answer层。Embed层负责将原文和问题中的tokens映射为向量表示；Encode层主要使用RNN来对原文和问题进行编码，这样编码后每个token的向量表示就蕴含了上下文的语义信息；Interaction层是大多数研究工作聚焦的重点，该层主要负责捕捉问题和原文之间的交互关系，并输出编码了问题语义信息的原文表示，即query-aware的原文表示；最后Answer层则基于query-aware的原文表示来预测答案范围。
• Match-LSTM -在模型实现上，Match-LSTM的主要步骤如下：
  • 1）Embed层使用词向量表示原文和问题，
  • 2）Encode层使用单向LSTM编码原文和问题embedding,
  • 3）Interaction层对原文中每个词，计算其关于问题的注意力分布，并使用该注意力分布汇总问题表示，将原文该词表示和对应问题表示输入另一个LSTM编码，得到该词的query-aware表
  • 4）在反方向重复步骤2，获得双向query-aware表示；
  • 5）Answer层基于双向query-aware表示使用SequenceModel或BoundaryModel预测答案范围。
• 模型之间的比较
  • 双层Interaction优于单层interaction机制，因为在原文-问题交互层之上的原文自交互层在部分程度上解决了长文本的长时依赖问题
  • 多轮推理机制，对于回答复杂问题具有一定的帮助，多轮推理机制可以不断缩小答案范围，最终定位正确的答案位置。
  • 对问题敏感的问题类型表示方法能更好的model各类问题，并根据问题类型聚焦原文中特定的词语
• Attention

其他

• MLE LSE MAP之间的关系
• 距离度量方法

最优化计算方法

• 最优化问题概述 *介绍最优化问题分类以及求解思路
• [线搜索方法] *基于线搜索方法，包括最速下降、牛顿方法以及步长计算等
• [信赖域方法] *介绍信赖域求解最优化问题的思路
• [共轭梯度方法] *介绍共轭方法的思路
• 拟牛顿方法 *介绍拟牛顿方法，用一阶梯度近似Hessian矩阵方法
• 大规模无约束最优化方法 *大规模无约束问题，LBFGS等
• 梯度计算  *复杂函数梯度近似方法
• 无梯度最优化方法 *不计算梯度情况下，如何进行最优化
• 最小二乘问题  *最优化方法应用，求解最小二乘问题
• 非线性方程  *最优化方法应用，求解非线性方程问题
• 有约束最优化问题  *介绍等式、非等式约束最优化问题以及最优化条件，包括KKT条件、对偶等
• 线性规划问题  *线性规划常见求解算法
• 非线性约束最优化问题  *介绍非线性约束的最优化问题求解思路
• 二次规划问题  *目标函数是二次函数的特殊最优化问题，是SQP、内点等方法的基础
• 惩罚和增广拉格朗日方法  *求解带约束最优化问题常用方法
• 序列二次规划和内点法  *SQP和IP方法对于求解大规模约束最优化问题提供方案

链接